zset的常用命令及应用场景
redis的有序集合zset用来存储一个或多个元素member及其对应分值score,并且会按照score由小到大的顺序进行排序。zset当中score可以重复,但是member不可以重复,当插入已存在的元素member时会覆盖之前member的score并进行重新排序。我们首先看下zset的主要操作命令
zadd key score member //插入元素
zscore key member //查询member的score值
zincrby key increment member //增加member元素的score
zcard key //元素member的个数
zcount key min max //score在min和max之间的元素个数
zrange key start stop //查询member索引在start和stop之间的元素
zrevrange key start stop //zrange的反向操作
zrangebyscore key min max //查询score在min和max之间的元素
zrevrangebyscore key min max //zrangebyscore的反向操作 score由大到小排序
zrank key member //member的排名
zrem key member //删除member元素
zremrangebyrank key start stop
zremrangebyscore key min max //按照member排名或者score范围删除元素
zrangebylex key min max //score相同时 字典序在min和max之间的元素
zcan key cursor
zunionstore dest num key1 key2 //取并集
zinterstore dest num key1 key2 //取交集
同样,zset的命令无外乎增删改查四种,只是删除和查询既可以根据member索引下标也可以根据score的范围;可以正向或者反向操作,这里正反向指的是根据score的排序方式;也可以查一个member元素的排名。
zset的应用场景有以下
- 延时队列。可以将任务作为zset的member,将任务的触发时间作为score插入zset当中,通过比较任务的触发时间来判断当前任务是否已经到了触发的时刻。
理论上,所有依赖排序,比如时间排序,数量排序的场景,包括获取数据对应排名的场景都可以使用zset,并且其时间复杂度可以控制在O(log n)。
zset的底层编码方式
与hash对象和list对象一样,zset在底层实际上维护着两种数据结构,ziplist和skiplist(实际还包括一个dict),通过两项配置来决定zset应该使用哪种数据结构
# Similarly to hashes and lists, sorted sets are also specially encoded in
# order to save a lot of space. This encoding is only used when the length and
# elements of a sorted set are below the following limits:
zset-max-ziplist-entries 128
zset-max-ziplist-value 64
当zset的member个数小于128并且所有的member所占空小于64byte时使用ziplist,否则使用skiplist。ziplist在 redis之hash实现 中已有详细描述,此处不再赘述。skiplist实际上是一个按照score排序的双向链表,这样我们可以对score和member的排名都可以精确或者范围查找,但是zscore或者zrank这类通过member来查询数据的操作在skiplist上没有办法,只能通过遍历查询,这样复杂度将达到O(n),所以,除了skiplist,zset还维护着一个dict,从member到score的映射,这样,对member的查询首先通过O(1)的时间复杂度查询到score,通过score再进行排名的查询,最终也可以达到O(log n)的时间复杂度。skiplist和dict的元素通过指针共享,因此不会浪费空间,同时在增加和删除元素的时候都需要对skiplist和dict进行操作,删除元素并且释放空间。 若zset对象编码为ziplist,在向其中增加元素的时候,会判断是否达到转为skiplist的条件。在执行zinterstore命令对zset进行计算交集的时候会判断是否将skiplist转为ziplist。
skiplist的理论分析
跳表(skiplist)可以看做是并联的有序链表,增删改查的复杂度都是O(log n),通常的有序链表在查找的时候一次跳过一个节点,skiplist拥有“多层”链表,在查找的时候一次可以跳过多个节点,层数越高跳过的节点数越多。首先我们看一个一般的有序链表,

查找的时候需要挨个节点遍历直到尾节点为止,辅复杂度为O(n)。插入是一样的,需要先进行查找操作。 假如我们给链表增加一层,这层链表的指针指向下下个节点,如下图

新增的这层链表的节点数只有原来的一般,上图中的7,19,26。当我们查找数据的时候沿着新链表查找,找到比待查数据大的节点的时候到下一层链表中继续查找,因为下一层指针跨越节点的粒度更细,比如我们要查找23的时候沿着图中红色的线进行查找。

查找的步骤如下,
- 在第一层链表中与7,19,26比较,发现比26小,则转向下一层链表继续查找;
- 在第二层链表中从19开始,与19,22,26相比,发现比26小,比22大,由于这层链表指针的节点跨度只有1,所以就确定了23的插入位置。
可以看到,整个查找过程避开了对3和11的查找,当随着链表层数越来越多的时候,可以避开的节点就会越来越多,有点类似二分查找。比如我们增加第三层链表,如下图

在我们查找23的时候,沿着最上层链表与19相比,23大于19,则继续向后查找,一次就越过了3,7,11这三个节点。可以想象,节点越多,链表层数越高的时候查询速度会越快。 但是这种链表在插入的时候有严重问题,由于每层链表的节点数有严格的比例关系,当我们新插入一个节点的时候,插入位置后面的节点的链表层数都需要调整,会将时间复杂度又变为O(log n)。比如我们在上图链表中再插入23这个节点,23之前的节点的链表层数不需要改动 ,只需要修改部分指针。但是23之后的节点链表层数都需要变化,并且相应指 针也需要重新指向。
为了解决这个问题,我们就不能要求每层链表之间有固定的比例关系,redis当中的skiplist在实现的时候,对于新增节点会随机出一个层数,比如3,就将这个节点链入1至3层的链表中,如下图我们演示一个插入过程。
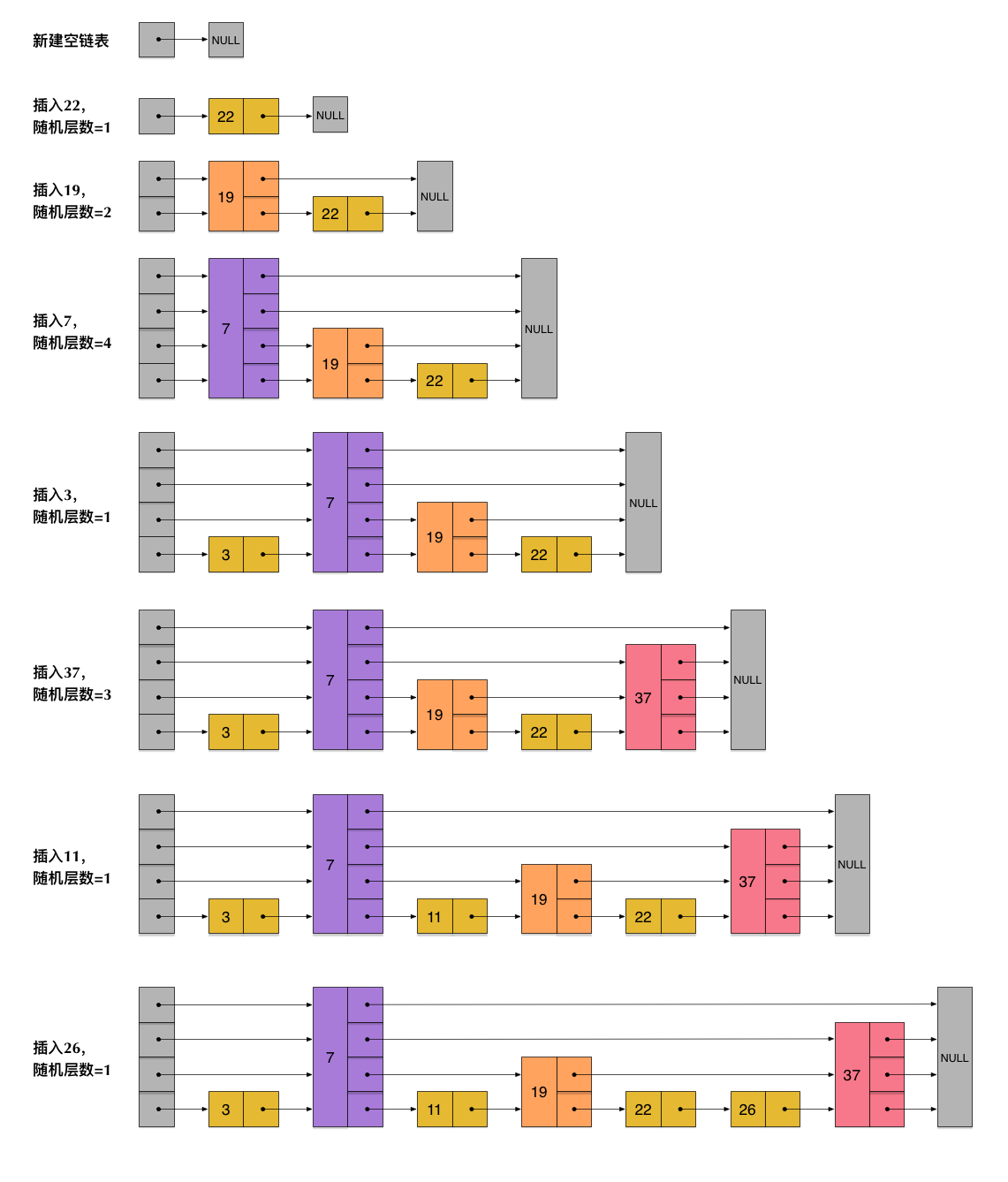
新插入节点不改变别的节点的层数,只需要修改每一层前后指针的指向。这样就降低了插入的复杂度。 与通常的跳表查找类似,redis的skiplist在查找的时候也是从最高层开始查起,当比查找元素大的时候就跳到下一层继续查找,由于每层的层数是随机的,这样就总会跳过一些节点,当跳到最底层链表的时候,就可以精确定位出元素的位置。 对于刚生产的skiplist,查找元素23的路径如下,
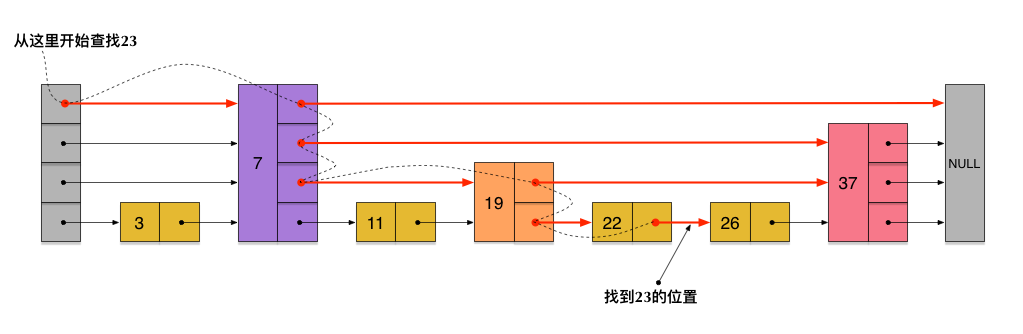
对于redis的zset,图中只展示了score,没有出现member,这并不妨碍我们分析zset的查找过程,因为zset就是一个以score排序的链表。
redis的skiplist的实现(包括主要的增删改查)
redis中的skiplist是如何实现增删改查的呢,下面我们通过源码分析一下,api主要在t_zset.c中。首先看一下zset所定义的基础数据结构
/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {
sds ele; //member
double score; //score
struct zskiplistNode *backward; //后向指针,用来反向遍历
struct zskiplistLevel {
struct zskiplistNode *forward;
unsigned long span; //当前层的指针跨越了几个节点
} level[]; //每个节点的所有链表层,包括指针及指针的跨度
} zskiplistNode;
typedef struct zskiplist {
struct zskiplistNode *header, *tail;
unsigned long length; //节点长度
int level; //skiplist的最高层数
} zskiplist;
//zset的实现包括skiplist和dict
typedef struct zset {
dict *dict;
zskiplist *zsl;
} zset;
对于skiplist中的每一个节点定义为 zskiplistnode,当中包含一个zskiplistLevel的结构体数组,对每个节点而言,这个数组记录了每一层链表的指向及到下一个节点的跨度。在我们做增加和删除操作的时候,主要需要更新这个数据。
向skiplist中插入节点
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
unsigned int rank[ZSKIPLIST_MAXLEVEL];
int i, level;
serverAssert(!isnan(score));
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
/* store rank that is crossed to reach the insert position */
rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
rank[i] += x->level[i].span;
x = x->level[i].forward;
}
update[i] = x;
}
/* we assume the element is not already inside, since we allow duplicated
* scores, reinserting the same element should never happen since the
* caller of zslInsert() should test in the hash table if the element is
* already inside or not. */
level = zslRandomLevel();
if (level > zsl->level) {
for (i = zsl->level; i < level; i++) {
rank[i] = 0;
update[i] = zsl->header;
update[i]->level[i].span = zsl->length;
}
zsl->level = level;
}
x = zslCreateNode(level,score,ele);
for (i = 0; i < level; i++) {
x->level[i].forward = update[i]->level[i].forward;
update[i]->level[i].forward = x;
/* update span covered by update[i] as x is inserted here */
x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}
/* increment span for untouched levels */
for (i = level; i < zsl->level; i++) {
update[i]->level[i].span++;
}
x->backward = (update[0] == zsl->header) ? NULL : update[0];
if (x->level[0].forward)
x->level[0].forward->backward = x;
else
zsl->tail = x;
zsl->length++;
return x;
}
插入包括以下步骤
- 最上面的for和while循环主要生成两个变量,update和rank,update是zskiplistNode的结构体数组,保存了插入位置在每一层的前一个节点。rank保存了在每一层上从头结点到插入位置的长度,也就是跨越的节点个数。for循环用来遍历层数,while循环用来在每一层查找要插入的位置。rank[i] = rank[i+1] 保证下一层能够继承上一层已经走过的长度,并在此基础上进行累加。
- 找到要插入的位置之后所随机生成层数,zslRandomLevel(),我们看下这个方法的实现
/* Returns a random level for the new skiplist node we are going to create.
* The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
* (both inclusive), with a powerlaw-alike distribution where higher
* levels are less likely to be returned. */
int zslRandomLevel(void) {
int level = 1;
while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
level += 1;
return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}
可以看到,random()&0xFFFF均匀分布在0-0xFFFF之间,生成一个level的概率是p,那么生成的层数为n(n < 32)的概率是p^n。
- 如果生成level的大于当前skiplist的level,初始化目前skiplist未达到的这些level
- 生成要插入的skiplist的节点
- for循环处理从0到新生成的level之间的每一层的操作,这个操作包括,将插入节点的前后节点指针重新指向,重新计算插入节点及前一个节点的跨度span。
- 如果生成的level小于当前skiplist的level,在这些层上,将前面每一个节点的跨度span加一
- 更新头尾指针,增加skiplist的长度。
删除skiplist节点
int zslDelete(zskiplist *zsl, double score, sds ele, zskiplistNode **node) {
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
int i;
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
x = x->level[i].forward;
}
update[i] = x;
}
/* We may have multiple elements with the same score, what we need
* is to find the element with both the right score and object. */
x = x->level[0].forward;
if (x && score == x->score && sdscmp(x->ele,ele) == 0) {
zslDeleteNode(zsl, x, update);
if (!node)
zslFreeNode(x);
else
*node = x;
return 1;
}
return 0; /* not found */
}
/* Internal function used by zslDelete, zslDeleteRangeByScore and
* zslDeleteRangeByRank. */
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
int i;
for (i = 0; i < zsl->level; i++) {
if (update[i]->level[i].forward == x) {
update[i]->level[i].span += x->level[i].span - 1;
update[i]->level[i].forward = x->level[i].forward;
} else {
update[i]->level[i].span -= 1;
}
}
if (x->level[0].forward) {
x->level[0].forward->backward = x->backward;
} else {
zsl->tail = x->backward;
}
while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
zsl->level--;
zsl->length--;
}
/* Free the specified skiplist node. The referenced SDS string representation
* of the element is freed too, unless node->ele is set to NULL before calling
* this function. */
void zslFreeNode(zskiplistNode *node) {
sdsfree(node->ele);
zfree(node);
}
在skiplist中删除一个节点包括三个步骤,找到要删除的元素,修改待删除节点前后的指针,释放待删除节点空间,下面具体分析
- 与插入元素一样,首先查找待删除元素的位置以及待删除节点在每一层的前一个节点,通过两层循环实现
- 比较待删除节点的score和member均相等时发起删除节点的操作
- 修改待删除节点的前向节点的forward指针及跨度span,backward指针,skiplist的长度及最高的level
- 释放待删除节点的空间
修改skiplist的节点
/* Remove and re-insert when score changes. */
if (score != curscore) {
znode = zslUpdateScore(zs->zsl,curscore,ele,score);
/* Note that we did not removed the original element from
* the hash table representing the sorted set, so we just
* update the score. */
dictGetVal(de) = &znode->score; /* Update score ptr. */
*flags |= ZADD_UPDATED;
}
/* Update the score of an elmenent inside the sorted set skiplist.
* Note that the element must exist and must match 'score'.
* This function does not update the score in the hash table side, the
* caller should take care of it.
*
* Note that this function attempts to just update the node, in case after
* the score update, the node would be exactly at the same position.
* Otherwise the skiplist is modified by removing and re-adding a new
* element, which is more costly.
*
* The function returns the updated element skiplist node pointer. */
zskiplistNode *zslUpdateScore(zskiplist *zsl, double curscore, sds ele, double newscore) {
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
int i;
/* We need to seek to element to update to start: this is useful anyway,
* we'll have to update or remove it. */
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
while (x->level[i].forward &&
(x->level[i].forward->score < curscore ||
(x->level[i].forward->score == curscore &&
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
x = x->level[i].forward;
}
update[i] = x;
}
/* Jump to our element: note that this function assumes that the
* element with the matching score exists. */
x = x->level[0].forward;
serverAssert(x && curscore == x->score && sdscmp(x->ele,ele) == 0);
/* If the node, after the score update, would be still exactly
* at the same position, we can just update the score without
* actually removing and re-inserting the element in the skiplist. */
if ((x->backward == NULL || x->backward->score < newscore) &&
(x->level[0].forward == NULL || x->level[0].forward->score > newscore))
{
x->score = newscore;
return x;
}
/* No way to reuse the old node: we need to remove and insert a new
* one at a different place. */
zslDeleteNode(zsl, x, update);
zskiplistNode *newnode = zslInsert(zsl,newscore,x->ele);
/* We reused the old node x->ele SDS string, free the node now
* since zslInsert created a new one. */
x->ele = NULL;
zslFreeNode(x);
return newnode;
}
修改skiplist节点的score,比如zincrby命令,需要删除原有节点,重新插入更新score之后的节点。下面分析下具体的步骤
- 在score确实有更新的情况下发起更新的操作,结束之后更新dict中member对应的score指针
- 更新操作时member及其对应的score必须存在于skiplist当中,首先找到要更新的节点和每一层对应的前向节点
- 如果更新score之后节点在skiplist中的位置不变,则直接更新节点score然后返回
- 否则删除当前节点,插入更新score之后的新节点并释放原节点的空间。
查询skiplist中的节点
/* Find the first node that is contained in the specified range.
* Returns NULL when no element is contained in the range. */
zskiplistNode *zslFirstInRange(zskiplist *zsl, zrangespec *range) {
zskiplistNode *x;
int i;
/* If everything is out of range, return early. */
if (!zslIsInRange(zsl,range)) return NULL;
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
/* Go forward while *OUT* of range. */
while (x->level[i].forward &&
!zslValueGteMin(x->level[i].forward->score,range))
x = x->level[i].forward;
}
/* This is an inner range, so the next node cannot be NULL. */
x = x->level[0].forward;
serverAssert(x != NULL);
/* Check if score <= max. */
if (!zslValueLteMax(x->score,range)) return NULL;
return x;
}
/* Finds an element by its rank. The rank argument needs to be 1-based. */
zskiplistNode* zslGetElementByRank(zskiplist *zsl, unsigned long rank) {
zskiplistNode *x;
unsigned long traversed = 0;
int i;
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
while (x->level[i].forward && (traversed + x->level[i].span) <= rank)
{
traversed += x->level[i].span;
x = x->level[i].forward;
}
if (traversed == rank) {
return x;
}
}
return NULL;
}
skiplist的查询有通过score查询的(zcount),有通过rank查询的(zrange)。无论是通过score查询还是通过rank查询,都要发挥skiplist的优势,就是从skiplist的最高层查起,两层for循环,外层对层数遍历,内层循环在每一层上通过对比score或者通过span来对比是否达到索引下标查询出符合条件的元素。
skiplist VS 平衡树
skiplist和平衡树的比较主要从三个方面来考虑,内存占用,插入节点复杂度,范围查找的支持
- 平衡树每个节点需要两个指针指向左右子树;对于skiplist,节点的平均高度level是1/(1-p),当p=1/4时,节点的平均高度1.33,平衡树在内存占用上没有优势。
- 平衡树的插入操作复杂,可能需要左右旋转来保证树的平衡;skiplist的插入相对简单,修改前后节点的指针即可。
- 无论是对score还是对排名进行范围查找,skiplist都可以很好的支持,包括zrank这类查询排名的操作,通过span属性都可以很好的解决;平衡树不具有顺序性,范围查找或者查询元素的排名在实现上都有一定的复杂度。
当然,skiplist也会有缺点,由于每层的level是随机生成的,很有可能skiplist的几层链表都是一样的或者层数很少,这样会使得查询复杂度高于O(log n),但还是优于 O(n)的,并且这种也属于极端情况,比较少见。
引文参考
- https://www.jianshu.com/p/cc379427ef9d
- https://blog.csdn.net/GDJ0001/article/details/80119209
- https://www.cnblogs.com/yuanfang0903/p/12165394.html
- https://blog.csdn.net/weixin_36194037/article/details/79440464